The FACT Function in Google Sheets (And Why A Shuffled Deck of Cards Is Unique)

Let’s start with a mind-blowing fact, and then use the FACT function in Google Sheets to explain it.

Pick up a standard 52 card deck and give it a good shuffle.

The order of cards in a shuffled deck will be unique.

One that has likely never been seen before in the history of the universe and will likely never be seen again.

I’ll let that sink in.

Isn’t that mind-blowing?

Especially when you picture all the crazy casinos in Las Vegas.

Let’s understand why, and in the process learn about the FACT function and basic combinatorics (the study of counting in mathematics).

Four Card Deck

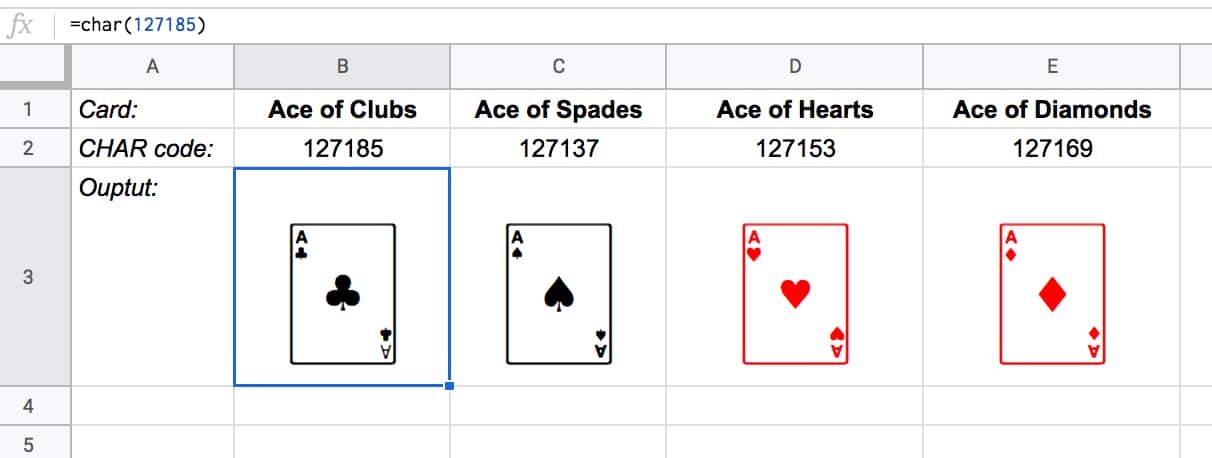
To keep things simple, suppose you only have 4 cards in your deck, the four aces.

You can create this deck in Google Sheets with the CHAR function:

The formulas to create these four cards are:

Ace of Clubs:

Ace of Spades:

Ace of Hearts:

Ace of Diamonds:

Let’s see how many different combinations exist with just these four cards.

Pick one of them to start. You have a choice of four cards at this stage.

Once you’ve chosen the first one, you have three cards left, so there are 3 possible options for the second card choice.

When you’ve picked that second card, you have two cards left. So you have a choice of two for the third card.

The final card is the last remaining one.

So you have 4 choices * 3 choices * 2 choices * 1 choice = 4 * 3 * 2 * 1 = 24

There are 24 permutations (variations) with just 4 cards!

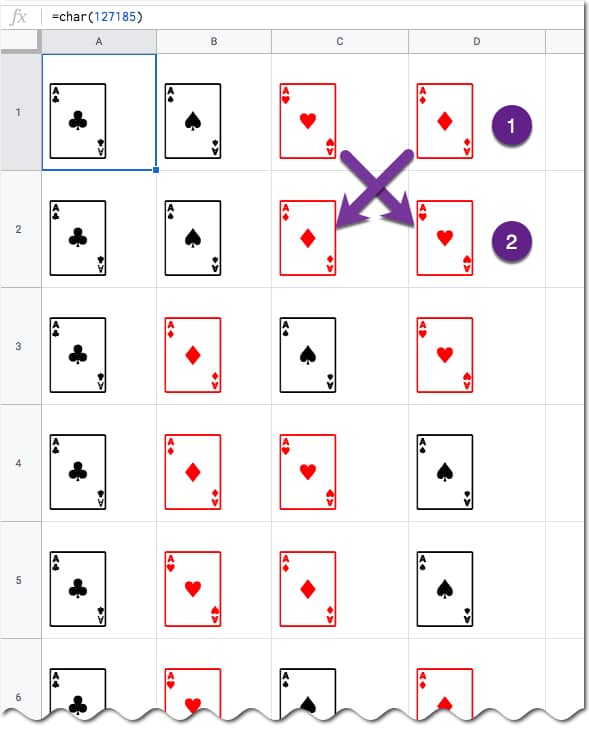
Visually, we can show this in our Google Sheet by displaying all the different combinations with the card images from above:

(I’ve just shown the first 6 rows for brevity.)

You can see for example, when moving from row 1 to row 2, we swapped the position of the two red suits: the Ace of Hearts and the Ace of Diamonds.

Five Card Deck

This time there are 5 choices for the first card, then 4, then 3, then 2, and finally 1.

So the number of permutations is 5 * 4 * 3 * 2 * 1 = 120

Already a lot more! I have not drawn this out in a Google Sheet and leave that as an optional exercise for you if you wish.

The FACT function

The FACT function in Google Sheets (see documentation) is a math function that returns the factorial of a given number. The factorial is the product of that number with all the numbers lower than it down to 1.

In other words, exactly what we’ve done above in the above calculations.

Four:

The 4 card deck formula is:

which gives an answer of 24 permutations.

Five:

The 5 card deck formula is:

which gives an answer of 120 permutations.

Six:

A 6 card deck is:

which gives an answer of 720 permutations.

Twelve:

A 12 card deck has  479,001,600 different ways of being shuffled:

(You’re more likely to win the Powerball lottery at 1 in 292 million odds than to get two matching shuffled decks of cards, even with just 12 cards!)

Fifty Two:

Keep going up to a full deck of 52 cards with the formula and it’s a staggeringly large number.

Type it into Google Sheets and you’ll see an answer of 8.07E+67, which is 8 followed by 67 zeros!

(This number notation is called scientific notation, where huge numbers are rounded to the first few digits multiplied by a 10 to the power of some number, 67 in this case.)

This answer is more than the number of stars in the universe (about 10 followed by 21 zeros).

Put another way if all 6 billion humans on earth began shuffling cards at 1 deck per minute every day of the year for millions of years, we still wouldn’t even be close to finding all possible combinations.